Newest↑
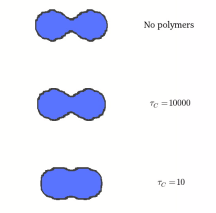
CELLS IN COMPLEX FLUIDS
My current project involves modelling cells moving and growing in a complex fluid. There are various ways to model cells, but two important factors to consider are that cells are motile, and that they swim in a non-Newtonian medium. The ultimate goal is to describe cell movement and growth using a minimal model that captures the essential physics of the biological system.My current project involves modelling cells moving and growing in a complex fluid. There are various ways to model cells, but two important factors to consider are that cells are motile, and that they swim in a non-Newtonian medium. The ultimate goal is to describe cell movement and growth using a minimal model that captures the essential physics of the biological system.My current project involves modelling cells moving and growing in a complex fluid. There are various ways to model cells, but two important factors to consider are that cells are motile, and that they swim in a non-Newtonian medium. The ultimate goal is to describe cell movement and growth using a minimal model that captures the essential physics of the biological system.My current project involves modelling cells moving and growing in a complex fluid. There are various ways to model cells, but two important factors to consider are that cells are motile, and that they swim in a non-Newtonian medium. The ultimate goal is to describe cell movement and growth using a minimal model that captures the essential physics of the biological system.
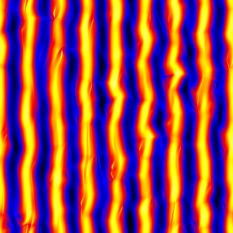
CHAOS AT LOW REYNOLDS NUMBER
I have studied how a minimal model of a polymer may bend in chaotic flows. First, I have shown that that a Brownian trumbbell (three-bead, two-rod) model can bend in an extensional flow (In fact it can perform a tumbling motion, even if such end-to-end reversal is only associated to shear flows). Using both analytical methods and numerical simulations, the bending dynamics of the polymer model is shown to be different in two and three dimensions. In particular, the trumbbell has two strong stable configurations in 2D but a clear preference for an extended configuration in 3D.

ELASTIC PARTICLES IN FLOWS
The COVID-19 disease is a major concern worldwide. Applied math modellers can help provide insight on its spread and suggest combinations of interventions to address this concern. When a vaccine is available, it is also important to know how to best distribute it given that its production will be limited at the start.

EPIDEMIOLOGY
The COVID-19 disease is a major concern worldwide. Applied math modellers can help provide insight on its spread and suggest combinations of interventions to address this concern. When a vaccine is available, it is also important to know how to best distribute it given that its production will be limited at the start.